STANDARD AAPRC4 AII Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 –y 2) 2 (2xy) 2 can be used to generate Pythagorean triples WORKSHEETS Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given (i) Area 25a2 – 35a 12 (ii) Area 35y2 13y – 12 Solution (i) We have, area of rectangle = 25a 2 – 35a12 = 25a 2 – a – 15a12Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
Www Jstor Org Stable
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples-Verify the identity sin 2 xtan 2x=tan 2 xsin 2x Which of the following four statements establishes the identity?Identity (x2y2)2 = (x2– y2)2 (2xy)2 can be used to generate Pythagorean triples HSMP7 Look for and make use of structure HSMP8 Look for and express regularity in repeated reasoning AAPR4 Understand that polynomial identities include but are not difference of two squares, the sum and difference of two cubes, the square of a



Www Jstor Org Stable
The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle; For x^2y^2=2xy, we get (by differentiating implicitly), dy/dx =1 That's the same as the derivative of a linear function with slope, 1 Hmmmmm Let's see If we have x^2y^2=2xy The we must also have x^22xy y^2=0 Factoring gets us (xy)^2 = 0 And the only way for that to happen is to have xy=0 So y=x and dy/dx =1 Find an answer to your question expand by using identity (2x y z)^2 hello sweet little pie we are going to play againare u online or not if yes then come fast I will start the game after 3/5 minutes Ok define trust
X 2sin x cos x A 2sin sin sinx tan2 x sin?x 스sin2xtan 2 xsin 2x sin2 xtan 2xsin2x cos XCOS X O B sin 2 xtan 2x= 2 cos x sin x O c sin 2 xtan 2x= sinxsin x 2 cosx sin x sinx cos*x O D sis sitan2 ahThe polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples SE/TE CB 318 AAPR5 () Know and apply the Binomial Theorem for the expansion of (x y)n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle SE/TE TE 330A330BStack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange
For example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Authors National Governors Association Center for Best Practices, Council of Chief State School Officers Y satisfying x y = 3 Let say y = 0 =>We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proved Show More Ex 25 Ex 25, 1 Ex 25,2 Important Ex 25,3 Important Ex 25,4This video shows how to expand using the identity '(xy)3=x3y33x2y3xy2'To view more EducationalTangent of x^22xyy^2x=2, (1,2) \square!



2



Even Fibonacci Numbers Problem 3 Largest Prime Factor Problem 4 Manualzz
For example, the polynomial identity (x 22 y 2) = (x2 – y ) (2xy) can be used to generate Pythagorean triples Use complex numbers in polynomial identities and equations MGSE912NCN8 Extend polynomial identities to include factoring with complex numbers For example, rewrite x2 4 as (x 2i)(x – 2i) STANDARDS FOR MATHEMATICAL PRACTICEExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicExample, the polynomial identity (x2 y2) 2 = (x2 – y 2) 2 (2xy)2 can be used to generate Pythagorean triples 8) AAPR6 Rewrite simple rational expressions in different forms;




Eisenstein Triples Studocu



2
Numerical relationships For example, the polynomial identity (x2 y2)2 = (x2 – y 2) (2xy) can be used to generate Pythagorean triples AAPR5 () Know and apply the Binomial Theorem for the expansion of (x y)n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example byFor example, the polynomial identity (x² y²)² = (x² – y²)² (2xy)² can be used to generate Pythagorean triples Lesson/Activity Lesson/Activity Description Suggested Technology The reference for Conic Section General Cartesian form tells you how to determine what conic section it is, when given the General Cartesian form #Ax^2 Bxy Cy^2 Dx Ey F = 0# Here is the given equation in the general form #2x^2 4y^2 8 = 0# Please observe the value of #B^2 4AC = 0^2 4(2)(4) = 32#The reference says that this is an ellipse



Pythagorean Triangles And Triples




Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions
Generate Pythagorean Triples using an identity About this video In this lesson you will learn to generate a Pythagorean Triple by using the identity (x^2 y^2)^2 (2xy)^2 = (x^2 y^2)^2Tap for more steps Add 1 1 to both sides of the equation x 2 y 2 2 x 2 y = 1 x 2 − y 2 − 2 x − 2 y = 1 Complete the square for x 2 2 x x 2 − 2 x Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = 2, c = 0 a = 1, b = − 2, c = 0Write a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less




Understanding Pythagorean Identities Studypug



Arxiv Org Pdf 1902
The polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples D Rewrite rational expressions AAPRD6 Rewrite simple rational expressions in different forms; Answer 2 📌📌📌 question The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3?For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Interpret functions that arise in applications in terms of the context MGSE912FIF4 Using tables, graphs, and verbal descriptions, interpret the key characteristics of a function which models the relationship



How To Find Pythagorean Triplets With One Given Number Quora




The Identity X2 Y22 X2 Y22 2xy2 Can Be Used To Gen Gauthmath
For example, the polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples D Rewrite rational expressions 6 Rewrite simple rational expressions in different forms;MGSE912AAPR4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples Video Lessons ( p1, p2a,And x>y (x2−y2)2 (2xy)2= (x2y2)2



Http Www Math Northwestern Edu Mlerma Problem Solving Putnam Training Problems 13 Pdf




Curiousmathsknols Mathematics For The Curious Page 2
Answer 2 📌📌📌 question The identity (x^2y^2)^2 = (x^2y^2)^2 (2xy)^2 can be used to generate pythagorean triples what pythagorean triple could be generated using x=8 and y=3 the answers to estudyassistantcomWrite a(x)/b(x) in the form q(x)Example, see x4 – y4 as (x2)2 – (y2)2, thus recognizing it as a difference of squares that can be factored as (x2 – y2) the polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples ( ) 1 a()/




Understanding Pythagorean Identities Studypug



2
Find dy/dx x^2y^2=2xy Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate Tap for more steps By the Sum Rule, the derivative of with respect to is Differentiate using the Power Rule which states that is whereIn this task students investigate and ultimately prove the validity of the method of generating Pythagorean Triples that involves the polynomial identity (x 2 y 2) 2 =(x 2y 2) 2 (2xy) 2 Type ProblemSolving TaskAdd − x 2 y 2 x 2 y 2 and x 2 y 2 x 2 y 2 Add x 2 x 2 x 2 x 2 and 0 0 Simplify each term Tap for more steps Multiply x 2 x 2 by x 2 x 2 by adding the exponents Tap for more steps Use the power rule a m a n = a m n a m a n = a m n to combine exponents Add 2 2 and 2 2



Http Www Veronaschools Org Cms Lib02 Nj Centricity Domain 18 Algebra 2 Pdf




Pdf Pythagorean Triples Before And After Pythagoras Ravi Agarwal Academia Edu
X2 y2 can be written as (xy)2 this is in the form of (a b)2 = a2 2ab b2 so the above can be written as x2 2xy y2 or there is another one too x2 y2 = (xy) (x yStudents will prove the polynomial identity ( x^2 y^2 )^2 ( 2xy )^2 = ( x^2 y^2 )^2 and use it to generate Pythagorean triples Use this activity as independent/partner practice or implement it as guided notes and practice for students in need of extra support This activity is in PDF format Part 1 Extension Activity (2 pages)Write a(x)/b(x) in the form q(x) r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the
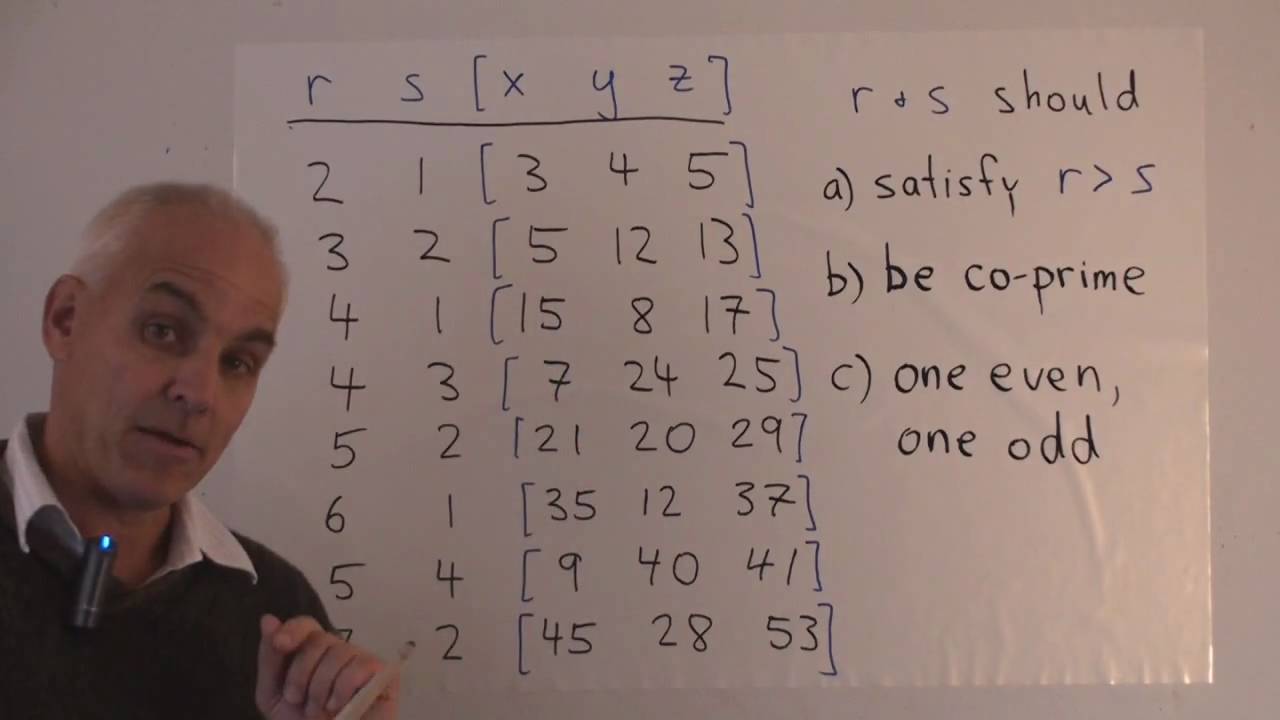



Pythagorean Triples Explanation Examples




How To Generate Pythagorean Triples Given The Sum Of The Triples Quora
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, the square of a binomial, etcCalculus Basic Differentiation Rules Implicit Differentiation Generate Pythagorean Triplets A Pythagorean triplet is a set of three positive integers a, b and c such that a 2 b 2 = c 2 Given a limit, generate all Pythagorean Triples with values smaller than given limit A Simple Solution is to generate these triplets smaller than given limit using three nested loop



Www Jstor Org Stable



Http Pgsd Org Cms Lib07 Pa Centricity Domain 43 Hs algebra 2 Pdf
For example, the polynomial identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples I can prove polynomial identitiesX 2 ( 1 2 y) x y 2 y − 2 Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and m divides the constant factor y^ {2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factorWrite a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) are



Http M Hikari Com Ijma Ijma 14 Ijma 33 36 14 Catarinoijma33 36 14 Pdf



1
Finding x and yintercepts given a polynomial function Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x2 y2)2 = (x2 y2)2 (2xy)2 can be used to generate Pythagorean triples TD Explan ation You have the quadratic equation 3x^2−10=−5 Then you must clear the variable "x" as below 3x^2−10=−5 3x^2=−510 3x^2=5 x^2=5/3 x= ±√ (5/3) When you multipy the numerator and the denominator by 3 for simplify the result, you obtain Identities V Last updated at by Teachoo Identity V is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca Let us prove it Proof (a b c) 2 = ( (a b) c) 2 Using (x y) 2 = x 2 y 2 2xy



2




Pythagorean Triples Keith Conrad Pdf Free Download
For example, the polynomial identity (x2 y2)2 = (x2 y2)2 (2xy)2 can be used to generate Pythagorean triples AAPRD Rewrite rational expressions AAPRD6 Rewrite simple rational expressions in different forms; How do you use Implicit differentiation find #x^2 2xy y^2 x=2# and to find an equation of the tangent line to the curve, at the point (1,2)?Let's solve this by graphing because I'm feeling a bit lazy with the latex My apologies You can see by the graph that we have 3 solutions for mathx/math and mathy/math We have (0,2),(0,math\sqrt{2}/math), and (0,math\sqrt{2}/mat




Formulas For Generating Pythagorean Triples Wikipedia
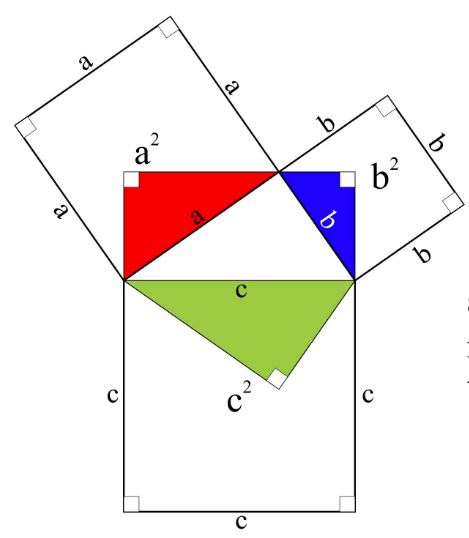



Pythagorean Theorem And Its Many Proofs
Let t = x 2 y 2 xy then t xy ≥ 0 since it is the sum of two real squares x 2 y 2 and t xy ≥ 0 since it is the square of the real (x y) since (x y) 2 = x 2 y 2 2xy adding these, we get 2t ≥ 0, therefore t ≥ 0Recognizing it as a difference of squares that can be factored as (x2 – y2)( x2 y2) Polynomial and rational ns at this level identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triplesX^ {2}2yxy^ {2}=0 x 2 2 y x y 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2y for b, and y^ {2} for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0




Pythagorean Theorem An Overview Sciencedirect Topics




Pdf Redefining And Classifying Primitive Pythagorean Triples
Identity (x2 y2)2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Desired Student Performance A student should know • Number theory • Consecutive numbers forms A student should understand I am trying to solve the equation $$ (x^2y^2)y' 2xy = 0 $$ I have rearranged to get $$ y' = f(x,y) $$ where $$ f(x,y) = \frac{2xy}{x^2y^2} $$ From here I tried to use a trick that I learned Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow,Identity (x2y2)2 = (x2– y2)2 (2xy)2 can be used to generate Pythagorean triples Eureka Math 1 Lesson 2 –7 Module 1 Lesson 10 MP1 Make sense of problems and persevere in solving them Students discover the value of equating factored terms of a polynomial to zero as a means of solving equations involving polynomials Eureka Math




Generating Pythagorean Triples Chilimath



Www Clarenceschools Org Cms Lib Ny Centricity Domain 465 Notes proving identities Pdf
X and y are positive integers;The answers to estudyassistantcom




Lesson 10 The Power Of Algebra Finding
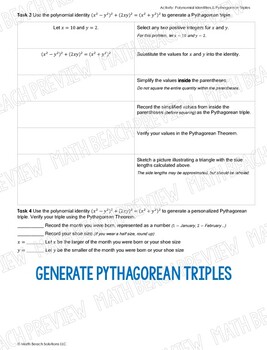



Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions




A Apr 4 Objective Adding Amp Subtracting Polynomials Prove Polynomial Identities And Use Them




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Q Tbn And9gcqj2x8ewakfrm0axkiwiis6syzwpxwp25x3mc26uqwe8y6xit7 Usqp Cau




Pythagorean Triple From Wolfram Mathworld
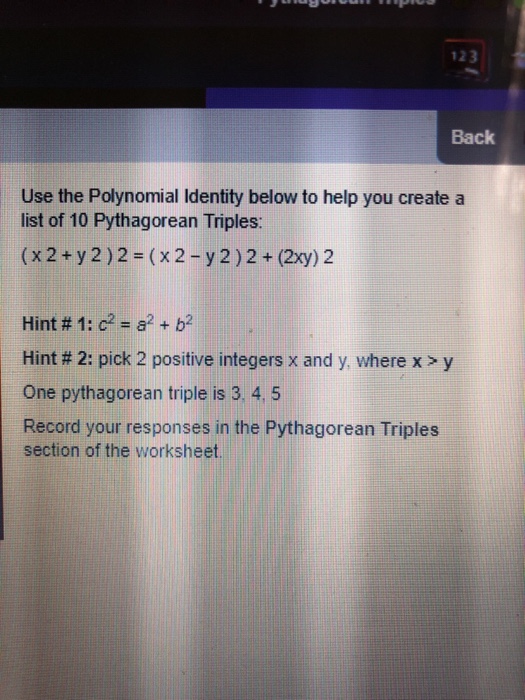



123 Back Use The Polynomial Identity Below To Help Chegg Com



Pythagorean Triples



Q Tbn And9gcqps6qllmp1l0vsb5diwencc9bdlyhgrbtu3gebndt6gzbuls2f Usqp Cau



Generating Pythagorean Triples Chilimath



Digitalcommons Gaacademy Org Cgi Viewcontent Cgi Article 1166 Context Gjs



Www Clarenceschools Org Cms Lib Ny Centricity Domain 465 Notes proving identities Pdf




7th Grade Problem Polynomial Exponentiation



Http Www Math Brown Edu Jhs Frintdir Frintch2ch3 Pdf



Math Questions Math Answers




Generate Pythagorean Triples Using An Identity Learnzillion




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



2



Www Kent K12 Wa Us Cms Lib Wa Centricity Domain 4229 Ksd algebra ii placemat Pdf



Www Jstor Org Stable 10 4169 College Math J 48 2 115
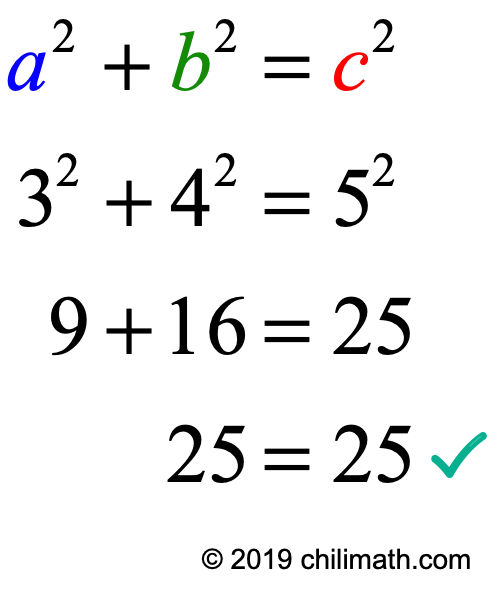



Generating Pythagorean Triples Chilimath




Answered Example 3 Jeremy Uses The Polynomial Bartleby




Pythagorean Theorem An Overview Sciencedirect Topics




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download




Calculus Set Free Infinitesimals To The Rescue Volume 1 Fall 19 Preliminary Edition By Bryan Dawson Issuu



Times Module M15 Pythagoras Theorem




Pythagorean Triplet In An Array Geeksforgeeks




Type The Correct Answer In Each Box In Part E You Proved That Any Pythagorean Triple Can Be Brainly Com




Use The Pythagorean Identity X2 Y 2 2xy 2 X2 Y2 2 To Create A Pythagorean Brainly Com



How To Find Pythagorean Triplets With One Given Number Quora



2




Polynomial Identities And Pythagorean Triples Activity Polynomials Algebra Resources Algebra 2 Activities
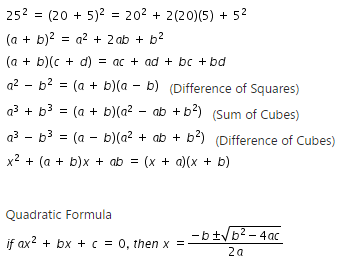



Mafs 912 A Apr 3 4 Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example The Polynomial Identity X Y X Y 2xy Can Be Used To Generate Pythagorean Triples




Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions




Polynomial Identities Solutions Examples Videos Worksheets Games Activities
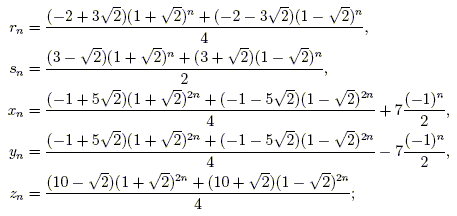



Pythagorean Triples




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Pythagorean Triples Generator Youtube



Pythagorean Triangles And Triples




Curiousmathsknols Mathematics For The Curious Page 2



2
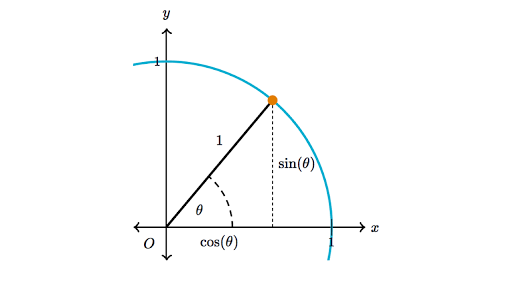



Pythagorean Identity Review Article Khan Academy



2



Www Brewtoncityschools Org Cms Lib Al Centricity Domain 133 8 2 The Pythagorean Theorem And Its Converse Pdf



2
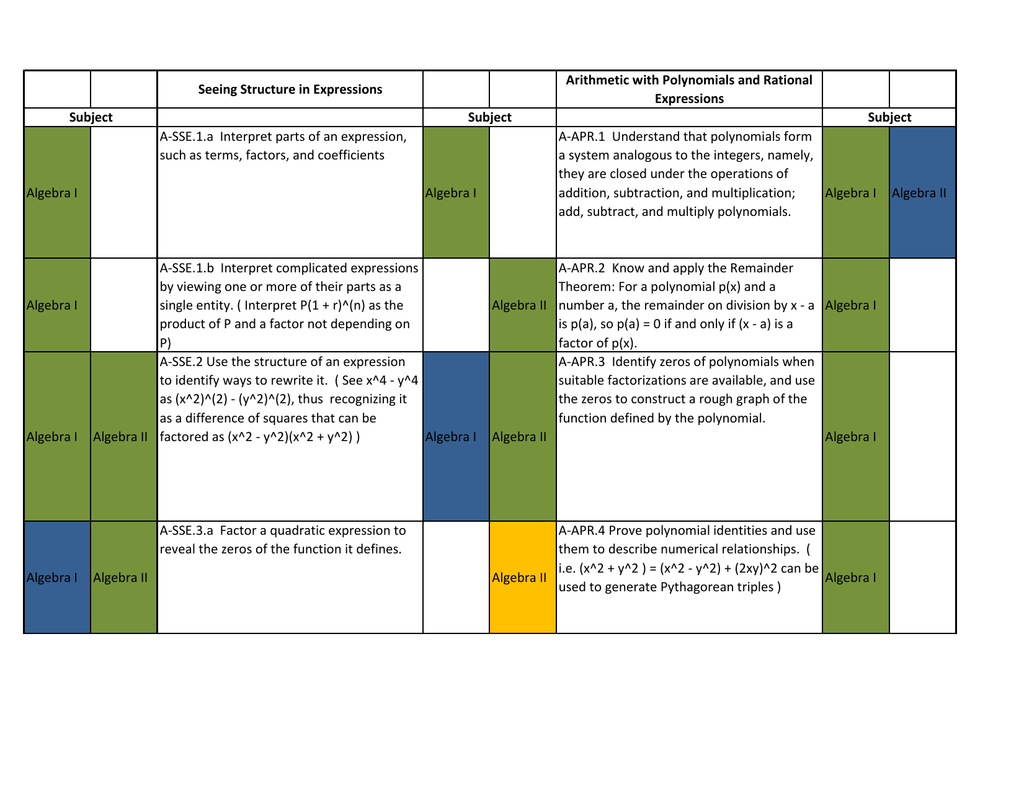



Seeing Structure In Expressions Arithmetic With Polynomials And
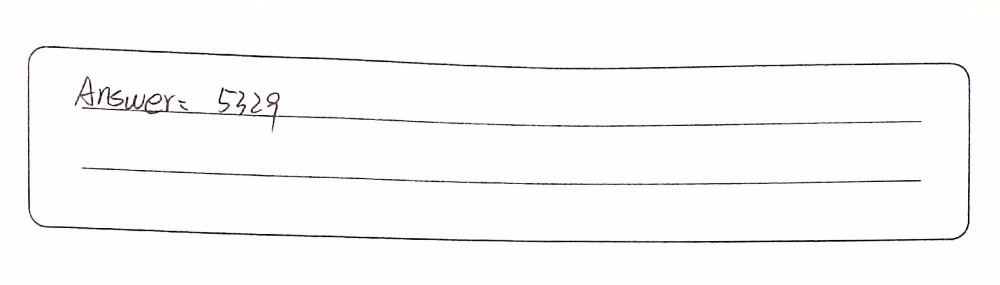



The Identity X2 Y22 X2 Y22 2xy2 Can Be Used To Gen Gauthmath




How To Use The Pythagorean Theorem With A Circle Veritas Prep
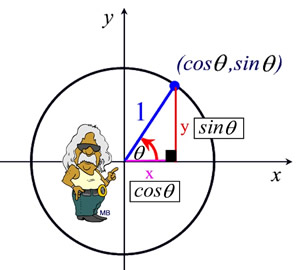



Pythagorean Identities Mathbitsnotebook Ccss Math



Webnew Ped State Nm Us Wp Content Uploads 21 07 Alg 2 Arithmetic With Polynomials And Rational Expressions Pdf



Times Module M15 Pythagoras Theorem



2



2




Pythagorean Theorem How To Use Pythagoras Theorem With Examples




Generating Pythagorean Triples 360




The Pythagorean Theorem Educational Outreach



2



Http Www Corestandards Org Assets Ccssi Mathematics Appendix A Pdf




Pythagorean Triple From Wolfram Mathworld



Q Tbn And9gcq4qz6q7ucw6zqek K4ieuig5j6stylu2ykwt8jbvvnyj35ga1g Usqp Cau




6 The Abc S Of Number Theory




Pythagorean Triples Video Lessons Examples Step By Step Solutions



Pythagorean Triple From Wolfram Mathworld




Pythagorean Theorem Wikipedia



2



Http Www Admschools Org Wp Content Uploads 15 10 12 05 May 14 12 07 Pdf




Pdf The Modular Tree Of Pythagoras



2




Pdf Pythagorean Triples Before And After Pythagoras



Www Fultonschools Org Cms Lib Ga Centricity Domain 1349 Algebra Ii Curriculum Map smf 19 Pdf



19 24 Use Implicit Differentiation To Find An Chegg Com




Pythagorean Triples Keith Conrad Pdf Free Download




Formulas For Generating Pythagorean Triples Wikipedia



Pythagorean Triangles And Triples



0 件のコメント:
コメントを投稿